Olá, candidatos! Frequentemente vemos nas provas de “Matemática e suas Tecnologias” questões que envolvem funções, sejam elas do 1° grau ou do 2° grau. Em alguns casos, podemos ver inclusive questões das provas de “Ciências da Natureza e suas tecnologias” que envolvem o conhecimento sobre funções. Vamos então relembrar alguns conceitos importantes para resolver qualquer tipo de questão com função no Enem.
Função do 1° Grau
Uma função do 1° grau ou função afim é do tipo f(x) = ax + b, com a e b , sendo que a é o coeficiente de x e b 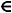
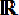 , o termo constante.
, o termo constante.
O zero ou a raiz da equação é o valor de x para o qual temos f(x) = 0. Então, se f(x) = ax + b e queremos encontrar f(x) = 0, faremos:
f(x) = 0
ax + b = 0
ax = – b
x = – b
a
Podemos dizer que a raiz de uma equação do 1° grau é dada por x = – b/a.
Função do 2° Grau
Uma função do tipo f(x) = ax² + bx + c, com a, b e c 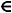
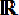 , é uma função do 2° grau ou função quadrática. Os termos a, b e c são ditos coeficientes, e a deve ser necessariamente diferente de zero (a ≠ 0) para que se tenha uma função do 2º grau.
, é uma função do 2° grau ou função quadrática. Os termos a, b e c são ditos coeficientes, e a deve ser necessariamente diferente de zero (a ≠ 0) para que se tenha uma função do 2º grau.
Ela pode ter até duas raízes ou zeros da equação. Para determinar quais são os valores de x, tais que f(x) = 0, nós utilizamos a fórmula de Bhaskara:
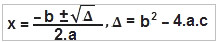
O gráfico de uma função do 2° grau é uma parábola. A partir de algumas fórmulas simples, podemos identificar os pontos notáveis da parábola. As coordenadas do vértice da parábola podem ser encontradas através de:
xv = – b
2a
yv = – Δ
4a
Agora que relembramos conceitos importantes sobre funções do 1° e do 2° grau, vamos resolver duas questões sobre função no Enem que caíram em provas anteriores.
1ª Questão com função no Enem de 2013
A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.
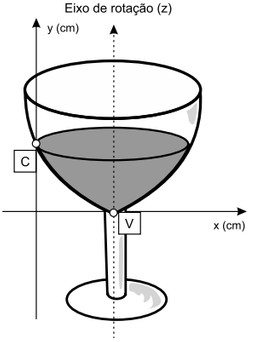
1ª questão com função – Enem 2013
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei 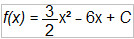 , onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x. Nessas condições, a altura do líquido contido na taça, em centímetros, é
, onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x. Nessas condições, a altura do líquido contido na taça, em centímetros, é
a) 1.
b) 2.
c) 4.
d) 5.
e) 6.
Resolução:
Conhecendo a função do 2° grau 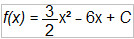 , seus coeficientes são a = 3/2, b = – 6 e c = C. Vamos então identificar as coordenadas do vértice V da parábola:
, seus coeficientes são a = 3/2, b = – 6 e c = C. Vamos então identificar as coordenadas do vértice V da parábola:
xv = – b
2a
xv = – (– 6)
2.(3/2)
xv = 6
3
xv = 2
yv = – Δ
4a
yv = – (b² – 4.a.c)
4a
yv = – [(– 6)² – 4.(3/2).C]
4.(3/2)
yv = – [36 – 2.3.C]
2.3
yv = – 36 + 6.C
6
yv = – 6 + C
Mas o vértice está localizado no eixo x, logo yv = 0, portanto, temos:
yv = – 6 + C
0 = – 6 + C
C = 6
A altura do líquido é de 6 cm, logo a alternativa correta é a letra e.
2ª Questão com função no Enem de 2011
O prefeito de uma cidade deseja construir uma rodovia para dar acesso a outro município. Para isso, foi aberta uma licitação na qual concorreram duas empresas. A primeira cobrou R$ 100 000,00 por km construído (n), acrescidos de um valor fixo de R$ 350 000,00, enquanto a segunda cobrou R$ 120 000,00 por km construído (n), acrescidos de um valor fixo de R$ 150 000,00. As duas empresas apresentam o mesmo padrão de qualidade dos serviços prestados, mas apenas uma delas poderá ser contratada.
Do ponto de vista econômico, qual equação possibilitaria encontrar a extensão da rodovia que tornaria indiferente para a prefeitura escolher qualquer uma das propostas apresentadas?
a) 100n + 350 = 120n + 150 ←
b) 100n + 150 = 120n + 350
c) 100(n + 350) = 120(n + 150)
d) 100(n + 350 000) = 120(n + 150 000)
e) 350(n + 100 000) = 150(n + 120 000)
Resolução:
Vamos identificar a primeira empresa descrita como Empresa A e a segunda como Empresa B. Podemos utilizar funções do 1° grau para descrever o preço cobrado por cada empresa. A empresa A tem um custo fixo de R$ 350 000,00 e cobra R$ 100 000,00 por km construído (n), então 350 000 é o termo constante e 100 000 é o coeficiente da variável n. A função que representa a empresa A é:
yA = an + b
yA = 100000.n + 350000
Para a empresa B, podemos afirmar que o custo fixo de R$ 150 000,00 é o termo constante e o valor de R$ 120 000,00 por km construído (n) é o coeficiente da variável n. Portanto, a função do preço cobrado pela empresa B é:
yB = an + b
yB = 120000.n + 150000
O valor cobrado pelas duas empresas será o mesmo quando yA = yB, então, temos:
yA = yB
100000.n + 350000 = 120000.n + 150000
Dividindo ambos os membros da equação por 1000, teremos:
100.n + 350 = 120.n + 150
A alternativa que apresenta a equação correta é a letra a.
Bons estudos!
Fontes:
Provas do Enem de 2013 e 2011.







